外观
Skip to content 查看源代码:
查看源代码:
water-20250805-KOI.md
---
title: 做韩国佬题目(KOI)
createTime: 2025/8/5
categories:
- IT
tags:
- OI
---
KOI Round 1 几乎全是暴力,纯属浪费感情。
以下是 Round 2,有些题依然很水。
## [P12661 [KOI 2023 Round 2] 不稳定数列](https://www.luogu.com.cn/problem/P12661)
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=3e5+100;
int a[maxn], f[maxn];
int la[2];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i=1; i<=n; i++){
cin >> a[i];
}
for (int i=1; i<=n; i++){
f[i] = f[la[1&~a[i]]] + 1;
la[1&a[i]] = i;
}
cout << max(f[la[0]], f[la[1]]);
return 0;
}
```
## [P12662 [KOI 2023 Round 2] 滑冰练习](https://www.luogu.com.cn/problem/P12662)
> 每个点都有一个速度限制 $V_i$。
> 可以任意提升速度,但若要降低速度,每次只能从上一个点的速度减少 $1$
$$
\max v_i = \min_{j \ge i}(V_j + j-i) = \min_{j \ge i}(V_j+j) - i
$$
计算 $V_j+j$ 的后缀最小值即可。
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5e5+100;
int V[maxn], m[maxn], ans;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i=1; i<=n; i++){
cin >> V[i];
}
// 最终速度
n++;
V[n] = 0;
m[n+1] = 0x3f3f3f3f3f3f3f3full;
for (int i=n; i>=1; i--){
m[i] = min(m[i+1], V[i] + i);
ans += m[i] - i;
}
cout << ans;
return 0;
}
```
[P12663 [KOI 2023 Round 2] 湖边的蚁穴
](https://www.luogu.com.cn/problem/P12663)
幻视基环树独立集。
> 注:方法为断一条环上的边。
> 由于边连接的两点至少有一个原图的最大独立集上出现
> 分别令两点为根并只计算根节点不选的最大独立集
> 然后取最大值即可。
本题:
两个选择:要么选择大房间不选小房间,要么选择小房间而不选大房间,
其他都不是最优的。
拆环 + 记录额外状态 + dp 即可。
状态设计:`f[上一个大房间是否被选择][第一个大房间是否被选择]`
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=25e4+100;
int c[maxn];
int f[2][2];
int f_copy[2][2];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i=1; i<=n; i++){
cin >> c[i];
}
f[1][1] = 1;
f[0][0] = c[1];
f[1][0] = f[0][1] = -0x3f3f3f3f3f3f3f3f;
for (int i=2; i<=n-1; i++){
memcpy(f_copy, f, sizeof f);
memset(f, -0x3f, sizeof f);
for (int r1=0; r1<=1; r1++) {
f[0][r1] = c[i] + max(f_copy[0][r1], f_copy[1][r1]);
f[1][r1] = 1 + f_copy[0][r1];
}
}
int ans = 1 + f[0][0];
for (int i=0; i<=1; i++) {
for (int j=0; j<=1; j++) {
ans = max(ans, c[n] + f[i][j]);
}
}
cout << ans;
return 0;
}
```
## [P12666 [KOI 2023 Round 2] 草地上的蚁穴](https://www.luogu.com.cn/problem/P12666)
来看看我写的题解吧。
!!洛谷似乎人手不够,直到 08-07 16:18 才过审!!
### 题意
定义树上的两个节点是和平的,当且仅当在它们之间增加一条边后最大独立集不变。求树上的和平点对数量。
### 分析
实际上不需要基环树上最大独立集的知识也能做。
正难则反。考虑那些不和平的对。在所有最大独立集中,它们必须都被选中。否则我们可以以一个不都被选中的独立集为基础加边,那么加边后这个集合仍为独立集。
因此,该问题实际上等价于求最大独立集必然包含的节点数 $M$,而答案即为所有点对减去不和平的点对,即 $\binom{N}{2} - \binom{M}{2}$。
如何寻找最大独立集必然包含的节点?
先求原树的最大独立集,再求不选某个点之后的最大独立集,若它们不等,则所有最大独立集必然包含这个点。
于是做法很明了了。换根 DP 即可。
#### 如果你不会换根 DP
- 把根节点换成与根节点相邻的节点时,其他节点的子树不会改变(如下图绿框)。
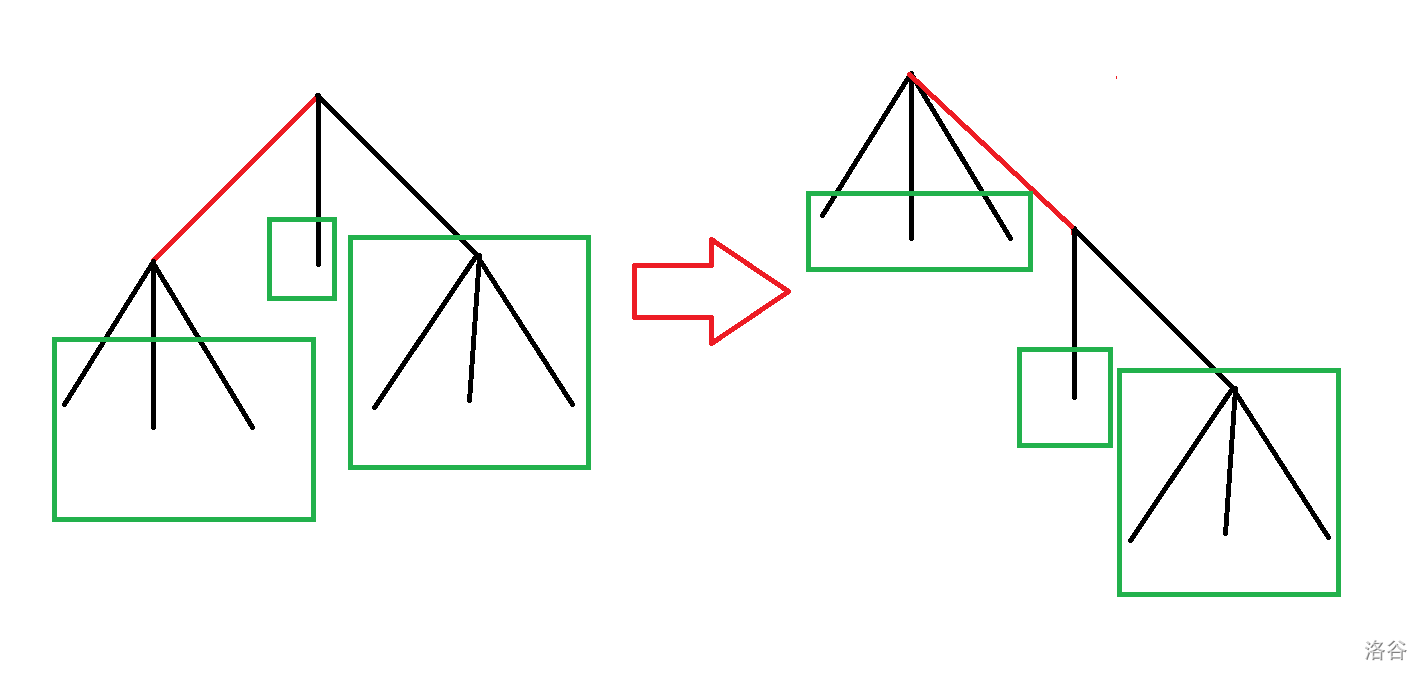
- 由于树形 DP 只局限于一个子树, 因此,这些子树的 DP 值也不会改变。
- 于是在换根之后,只需重新计算*两个节点的 DP 值即可。
> *请注意:
> 不能直接重新计算,否则会被菊花图卡成 $O(n^2)$。
> 但是变化的部分也只有这两个节点。因此,计算出换根前后加或减了哪一项是 $O(1)$ 的。
### 代码
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long // 有 N*(N-1)/2 的计算
const int maxn = 25e4+100;
vector<int> G[maxn];
int f[maxn][2]; // f[当前节点][当前节点选不选]
int tmp[2];
int mis, m;
void dfs(int u, int fa) {
f[u][0] = 0;
f[u][1] = 1;
for (int v: G[u]) {
if (v == fa) {
continue;
}
dfs(v, u);
f[u][0] += max(f[v][0], f[v][1]);
f[u][1] += f[v][0];
}
}
inline void chroot(int old_root, int new_root) {
// 先把边断掉
f[old_root][0] -= max(f[new_root][0], f[new_root][1]);
f[old_root][1] -= f[new_root][0];
// 再建立新边
f[new_root][0] += max(f[old_root][0], f[old_root][1]);
f[new_root][1] += f[old_root][0];
}
void dp(int u, int fa) {
if (fa != -1) {
chroot(fa, u);
}
if (f[u][0] != mis) {
m++;
}
for (int v: G[u]) {
if (v != fa) {
dp(v, u);
}
}
if (fa != -1) {
chroot(u, fa);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i=1; i<=n-1; i++) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1, -1);
mis = max(f[1][0], f[1][1]);
dp(1, -1);
cout << (n*(n-1)/2 - m*(m-1)/2);
return 0;
}
```