概述

在树形 DP 问题中，许多问题最初都是通过固定一个根节点进行递推求解的。然而，有些题目要求计算以每一个节点为根时的答案。若对每个节点重新执行一次完整的 DP 过程，时间复杂度将达到 $O(n^2)$，在节点数较多时往往无法接受。

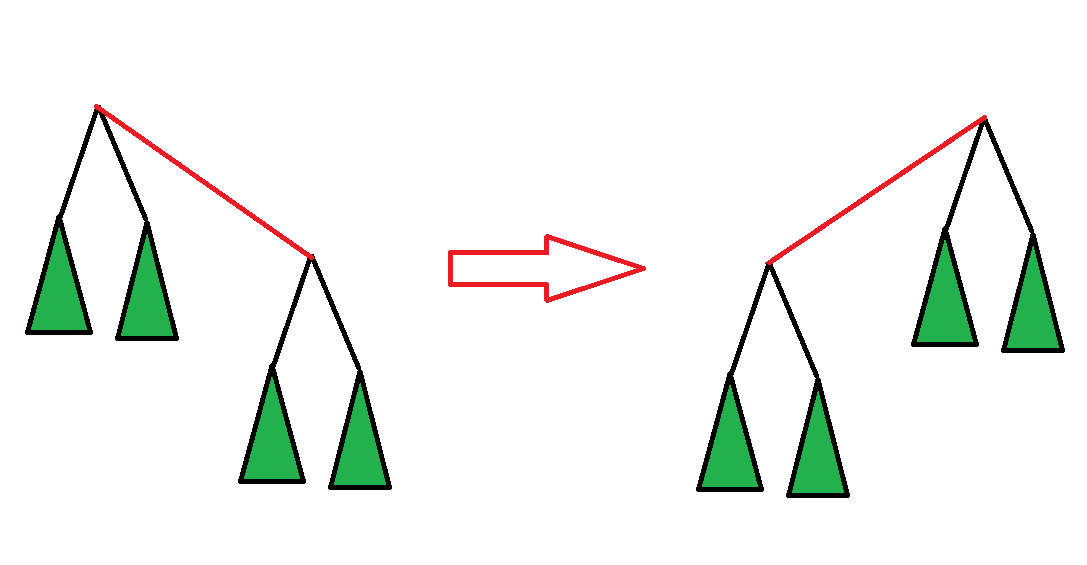
观察发现，当根节点从一个节点 $u$ 调整到其相邻节点 $v$ 时，实际上只有 $u$ 和 $v$ 两个节点的 DP 值会发生变化，而其他子树（如图中绿色部分）的 DP 值保持不变。因此，我们可以通过一次遍历，在相邻节点之间逐步“转移”根节点，从而高效地计算出所有节点作为根时的 DP 值。

删边-重建换根法

若每次换根时都暴力重新计算旧根和新根的 DP 值，在菊花图等极端情况下单次换根可能达到 $O(n)$ 的时间复杂度。为了避免这种情况，我们可以利用 DP 转移方程的性质：如果该方程支持动态添加或移除某个子树的贡献，则换根过程可以分两步完成：

1. 从旧根中移除新根子树的贡献；
2. 在新根中加入旧根子树的贡献（把旧根作为新根的一个新子树）。

这一过程相当于先删除旧根与新根之间的边，再重建一条反向的边，从而实现根的高效切换，如下图所示：

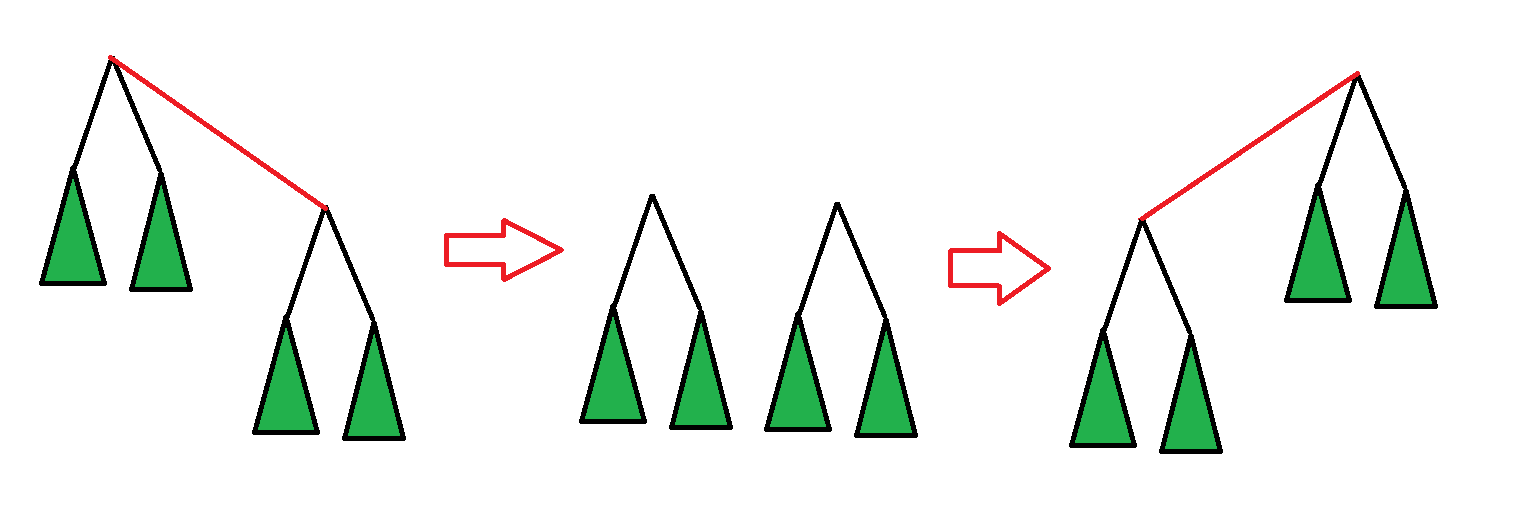
示例

以 P12666 [KOI 2023 Round 2] 草地上的蚁穴 中的最大独立集问题为例，换根操作可以通过以下方式实现：

inline void chroot(int old_root, int new_root) {
    // 先把边断掉 
    f[old_root][0] -= max(f[new_root][0], f[new_root][1]);
    f[old_root][1] -= f[new_root][0];
    
    // 再建立新边
    f[new_root][0] += max(f[old_root][0], f[old_root][1]);
    f[new_root][1] += f[old_root][0];
}

撤销换根法

如果 DP 转移关系较为复杂，不支持直接加减子树的贡献，又该如何处理？

这里可以借鉴一个（我编的）笑话：

Theorem. 所有数据结构都支持撤销操作。
Proof. 只需用一个栈记录每次覆盖操作前的状态，即可实现回退。

基于这一思想，我们可以对二次扫描过程进行优化：

• 在第一次访问某节点时，正常计算其 DP 值；
• 当从该节点回溯时，通过记录的历史状态撤销当前操作，恢复到该节点未被访问时的状态。

这样，在换根过程中，我们只需在回溯时执行撤销，即可避免重复计算。

该方法的总时间复杂度和空间复杂度与常规树形 DP 相同，但常数可能略大。

示例

同样以 P12666 [KOI 2023 Round 2] 草地上的蚁穴 中的最大独立集问题为例，撤销换根法的实现如下：

// 可以复用 DP1 的代码
inline void calc(int u, int fa) {
    f[u][0] = f[u][1] = 0;  // __不清空，_____

    for (int v: G[u]) {
        if (v == fa) { continue; }

        f[u][0] += max(f[v][0], f[v][1]);
        f[u][1] += f[v][0];
    }
}

inline void record(int *x, int *y) {
    x[0] = y[0]; x[1] = y[1];
}

void dp2(int u, int pre) {
    m += (f[u][0] == f[u][1]);

    for (int v: G[u]) {
        if (v == pre) { continue; }

        // 记录当前状态
        int r1[2], r2[2];
        record(r1, f[u]);
        record(r2, f[v]);

        // 换根 u->v
        calc(u, v);
        calc(v, -1);

        dp2(v, u);

        // 撤销换根
        record(f[u], r1);
        record(f[pre], r2);
    }
}