P11554 [ROIR 2016] 假期旅行 (Day 1)

（与那个动态删边的线段树分治）一样地，考虑可用的区间（最多 $m+k$ 个），贪心地，每次在可达的区间中选择右端点最远的那个。

于是可以预处理一个 $\mathrm{ext}(R)$，代表当前右端点范围内的区间可以扩展到的最远右端点。有转移方程

$$\mathrm{ext}(R) = \max_{l \le R} r(l) = \max \{\mathrm{ext}(R-1), \max r(l=R)\}$$

更进一步地，预处理出一个 $\mathrm{ext}^{2k}(R)$，利用倍增快速扩展右端点。若扩展 $n$ 步仍不可到达则说明无解。

时间复杂度 $O(n \log n)$（$n, m, k, q$ 同级）

坑：输入数据无序，需要排序（但是样例有序）

#include <bits/stdc++.h>
using namespace std;

namespace safeNS {
    const int maxn=2e5+100, maxlogn=20;
    
    struct ticket {
        int s, t;
        bool operator < (const ticket &b) const {
            return s < b.s;
        }
    };
    
    int n, m, k, logn;
    vector<ticket> sold[maxn];
    int rof[maxn];
    int ext[maxn][maxlogn];
    
    inline void add_free(int l, int r) {
//      printf("insert(%d, %d) %s\n", l, r, (l>r)?"ignored.":"OK.");
        rof[l] = max(rof[l], r);
    }
    
    void pre() {
        for (int __n=1; __n <= n;) {
            __n <<= 1;
            logn++;
        }
        
        for (int i=1; i<=n; i++) {
            rof[i] = i;
        }
        
        for (int a=1; a<=k; a++) {
            // 坑：输入数据无序（但是样例有序） 
            sort(sold[a].begin(), sold[a].end());
            
            if (sold[a].empty()) {
                add_free(1, n);
                continue;
            }
            
            add_free(1, sold[a].front().s);
            add_free(sold[a].back().t, n);
            for (int i=0; i<sold[a].size()-1; i++) {
                add_free(sold[a][i].t, sold[a][i+1].s);
            }
        }
        
        for (int i=1; i<=n; i++) {
            ext[i][0] = max(rof[i], ext[i-1][0]);
        }
        
        for (int lv=1; lv<=logn; lv++) {
            for (int i=1; i<=n; i++) {
//              printf("ext(%d, %d)", i, lv);
                ext[i][lv] = ext[ext[i][lv-1]][lv-1];
//              printf(" = %d\n", ext[i][lv]);
            }
        }
    }
    
    int solve(int l, int r) {
        int ans = 0;
        
        for (int lv=logn; lv>=0; lv--) {
            if (ext[l][lv] < r) {
                l = ext[l][lv];
                ans += 1 << lv;
            }
        }
        
        if (ext[l][0] >= r) {
            return ans + 1;
        }
        return -1;
    }
    
    int main() {
        ios::sync_with_stdio(0);
        cin.tie(0); cout.tie(0);
        
        cin >> n >> m >> k;
        for (int i=1; i<=m; i++) {
            int s, t, a;
            cin >> s >> t >> a;
            sold[a].push_back({s, t});
        }
        
        pre();
        
        int q;
        cin >> q;
        for (int i=1; i<=q; i++) {
            int f, d;
            cin >> f >> d;
            cout << solve(f, d) << '\n';
        }
        
        return 0;
    }
}

int main() {
    return safeNS::main();
}

P11557 [ROIR 2016] 有趣数字 (Day 2)

一个显然的数位 dp 板子，就当是复习数位 dp 了。

首先前缀和化，转化为求 $\mathrm{ans}(r) - \mathrm{ans}(l-1)$。

然后，设状态 $f(i, j, 0/1)$ 表示前 $i$ 位，最后一位为 $j$，且前 $i$ 位是/否与上界相同的方案数。

则

$$\begin{aligned} f(0, 0, 1) &= 1\\ f(i, a_i, 1) &= [a_{i-1} \le a_i]f(i-1, a_{i-1}, 1) \\ f(i, j, 0) &= \left( \sum_{k=0}^{j} f(i-1, k, 0) \right) + [a_{i-1} \le j < a_i]f(i-1, a_{i-1}, 1) \end{aligned}$$

前导零在本题是无害的。

时间复杂度 $O(b^2 \mathrm{len})$，在本题中 $b=10$。

#include <bits/stdc++.h>
using namespace std;

namespace safeNS {
    const int maxn=128, mod=1000000007;
    
    char cl[maxn], cr[maxn];
    int l[maxn], r[maxn];
    int f[maxn][12][3];
    
    int solve(int n, int *a) {
        memset(f, 0, sizeof(f));
        f[0][0][1] = 1;
        
        for (int i=1; i<=n; i++) {
            if (a[i-1] <= a[i]) {
                f[i][a[i]][1] = f[i-1][a[i-1]][1];
            }
            
            int sum=0;
            for (int j=0; j<=9; j++) {
                sum += f[i-1][j][0];
                sum %= mod;
                f[i][j][0] = sum;
                if (j < a[i] && a[i-1] <= j) {
                    f[i][j][0] += f[i-1][a[i-1]][1];
                    f[i][j][0] %= mod;
                }
//              printf("f(%d, %d) = %d\n", i, j, f[i][j][0]);
            }
        }
        
        int ans=f[n][a[n]][1];
        for (int i=0; i<=9; i++) {
            ans += f[n][i][0];
            ans %= mod;
        }
        return ans;
    }
    
    void reduce(int n, int *a) {
        for (int i=n; i>=1; i--) {
            if (a[i] == 0) {
                a[i] = 9;
            } else {
                a[i]--;
                return;
            }
        }
    }
    
    int main() {
        ios::sync_with_stdio(0);
        cin.tie(0); cout.tie(0);
        
        cin >> cl+1 >> cr+1;
        int nl = strlen(cl+1),
            nr = strlen(cr+1);
        
        for (int i=1; i<=nl; i++) {
            l[i] = cl[i] - '0';
        }
        for (int i=1; i<=nr; i++) {
            r[i] = cr[i] - '0';
        }
        
        reduce(nl, l);
        cout << (solve(nr, r) - solve(nl, l) + mod) % mod << '\n';
        
        return 0;
    }
}

int main() {
    return safeNS::main();
}

P11122 [ROIR 2024] 表格游戏 (Day 1)

看到数据范围极小，先考虑状压选择的行（dfs 是等效的）。

如果再状压列，就发现变成 $O(2^{2n})$，寄了。

这种子序列（某种可拆分性质）存在性问题可以用折半搜索。先搜前一半，再搜后一半，然后看看有没有前后匹配的。

时间复杂度 $O(n \cdot 2^{3n/2})$

#include <bits/stdc++.h>
using namespace std;

#define int long long  // 不安全但是忍不住 
#define __CHECK_ANS__ do {if (ans) { return; }} while (0)
// 保护现场 

namespace safeNS {
    const int maxn=20;
    int h, w, s, mid;
    int a[maxn][maxn];
    int r[maxn];
    
    bool ans=false;
    bool cr[maxn], cc[maxn];
    
    map<int, int> st;
    void dfs2(int i, int sum, int state) {
        if (i == mid + 1) {
            st[sum] = state;
            return;
        }
        dfs2(i+1, sum, state);
        dfs2(i+1, sum + r[i], state|(1<<i));
    }
    
    void dfs3(int i, int sum) {        
        if (i == w + 1) {
            if (st.count(s - sum)) {
                ans = true;
                // 解码状态 
                for (int j=1; j<=mid; j++) {
                    cc[j] = (st[s-sum] >> j) & 1;
                }
            }
            return;
        }
        
        dfs3(i+1, sum);
        __CHECK_ANS__;
        
        cc[i] = true;
        dfs3(i+1, sum + r[i]);
        __CHECK_ANS__;
        cc[i] = false;
    }
    
    void dfs1(int i) {
        if (i == h + 1) {
            st.clear();
            dfs2(1, 0, 0);
            dfs3(mid+1, 0);
            return;
        }
        
        dfs1(i+1);
        __CHECK_ANS__;
        
        cr[i] = true;
        for (int j=1; j<=w; j++) {
            r[j] += a[i][j];
        }
        
        dfs1(i+1);
        __CHECK_ANS__;
        
        cr[i] = false;
        for (int j=1; j<=w; j++) {
            r[j] -= a[i][j];
        }
    }
    
    signed main() {
        ios::sync_with_stdio(0);
        cin.tie(0); cout.tie(0);
        
        cin >> h >> w;
        mid = w / 2;
        for (int i=1; i<=h; i++) {
            for (int j=1; j<=w; j++) {
                cin >> a[i][j];
            }
        }
        cin >> s;
        
        dfs1(1);
        
        cout << (ans? "YES\n": "NO\n");
        
        if (ans) {
            int k=0;
            for (int i=1; i<=h; i++) {
                k += (!cr[i]);
            }
            for (int i=1; i<=w; i++) {
                k += (!cc[i]);
            }
            cout << k << '\n';
            
            for (int i=1; i<=h; i++) {
                if (!cr[i]) {
                    cout << "1 " << i << '\n';
                }
            }
            for (int i=1; i<=w; i++) {
                if (!cc[i]) {
                    cout << "2 " << i << '\n';
                }
            }
        }
        
        return 0;
    }
}

signed main() {
    return safeNS::main();
}

P11126 [ROIR 2024] 三等分的数组 (Day 2)

先造个桶 $c(i)$，然后设 $f(i,j,k)$ 为 $i-2$ 用完，$i$ 剩 $j$ 个，$i-1$ 剩 $k$ 个的方法数，根据转移图示，有

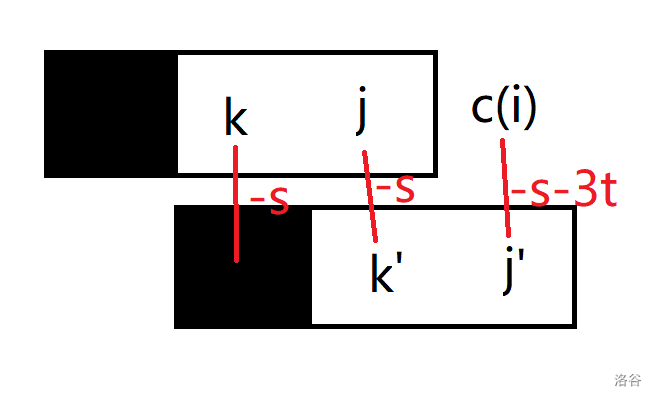
$$\begin{aligned} f(i,j,k) \to f(i+1, c(i)-k-3t, j-k) \end{aligned}$$

做一个前缀和，把 $t$ 这维优化掉即可（静态求值会搞出二维前缀和，不如正向递推）

时间复杂度 $O(m c^2)$，但如果认为这是立方级的算法就错了（我之前是这么认为的(汗，直到打开了题解）。

根据爱因斯坦的结论，$O(m c^2) = O(E)$

根据排序不等式，$\sum c(i)c(i+1) \le \sum [c(i)]^2 \le \bigl[ \sum c(i) \bigr]^2 = n^2$，$O(n^2)$ 的复杂度可以接受。

记得开滚动数组，不然 MLE 警告。