外观
末地超宏观结构的形成原理
最近(并非最近)流传着这样一张末地的图片:

这张图中的末地不是均匀的,而是呈一个个同心圆环套起来的规律形状。那这是什么原理呢?
末地环
末地生成机制
MC 生成末地的时候,是以 8×8 的小块为单位确定地形高度的。
确定高度的时候,会计算当前 8×8 小块计算离末地中心的距离 8⌊8x⌋2+⌊8z⌋2,以此确定末地岛的基准高度。
这个高度决定机制将是我们理解末地环的关键。
溢出与开方
然而,Mojang 写代码的时候,似乎忽略了一个东西:整数类型会溢出。
注意
只有整数类型有这样的溢出现象。
浮点数的距离现象与整数溢出不同:浮点数使用二进制科学记数法,当数字数量级增大时,由于小数位数有限,会导致很大的误差。
什么是溢出?以 32 位整数为例,32 位只能表示 −231∼231−1 的整数。那如果在运算的过程中出现了比 231−1 更大的数呢?
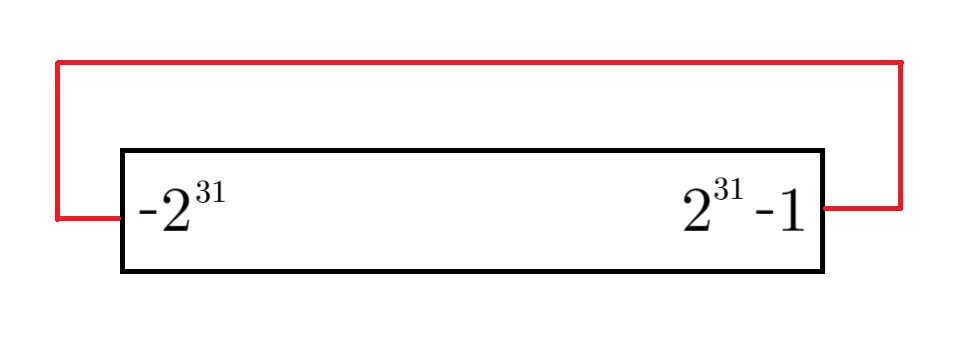
如图所示,当运算的过程中出现了比 231−1 更大的数,就会发生溢出,从最小值开始继续增加。
如果 ⌊8x⌋2+⌊8z⌋2 溢出成负数,那么开方就会失败,就形成了环状虚空。
末地环半径公式
要判断 X 在计算机中溢出成正数还是负数,只需判断 ⌊231X⌋ 是奇数还是偶数。如果是奇数,X 就会溢出成负的,否则就是正的。
于是有公式
rn=8⌊8x⌋2+⌊8z⌋2=8231n=2182n
在 r2k−1∼r2k 之间是正常的地形,而在 r2k+1∼r2k 之间是虚空。
注
主岛周围的虚空属于正常地形。
根据公式,可以得到 r1=2182n≈370727.6,与实验结果相符。
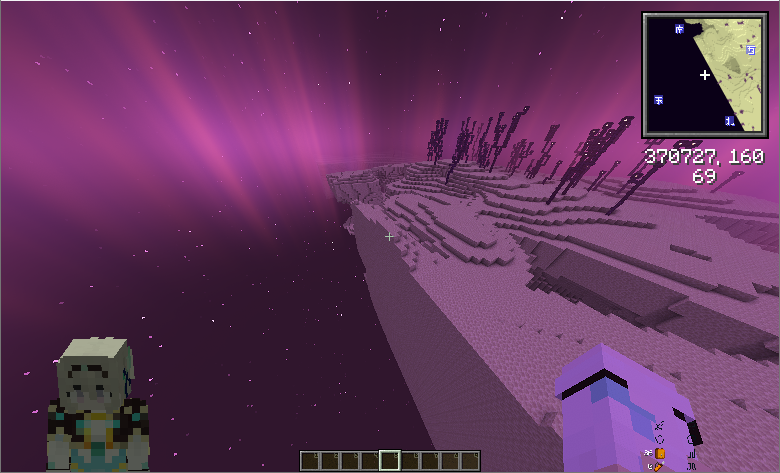
提示
坐标偏差是因为坐标除以 8 有下取整。精确的坐标为 x=8×⌊8370727.6⌋=370720。
多重溢出与末地环群
在以上的推导中,我们假定了只有 r2 有溢出现象。如果 ⌊8x⌋ 或者 ⌊8x⌋2 溢出,又会导致什么现象呢?
我们都知道,根据二项式定理,
(x+231)2≡x2+232x+262≡x2(mod232)
于是 x2 在溢出意义下有 231 的周期。
由此,我们可以推知,末地存在周期为 8×231=234 的四方连续重复。
下图展示了 6 位整数下的末地环群:

虽然该坐标过于遥远而无法到达,但是仍然可以通过模组等方法观察到这样的重复现象。而我们只是用计算,便揭示了它的存在——这就是数学的魅力。
噪声与末地类晶体结构
一篇文章显示,末地存在更大尺度的结构,这并不是计算和原点的距离引起的。
这涉及末地生成的另外的机制:噪声。
注意
由于噪声是以区块为单位的,除非特别说明,以下推导中的坐标均为区块坐标。
噪声算法
首先,我们得知道噪声是如何工作的。
如果让你写一个算法,来生成一个随机的连续函数,你会怎么写?
直接用把各点的取值设置为随机值显然不行。不难想到,先确定函数在各个点的取值,再用平滑的曲线将相邻两点连起来。
我们可以将这样的思路推广到二维。为了保证各向同性,我们将平面分割为正三角形网格,并为每一个格点赋予一个随机值。接下来,对于一个点,我们可以找到它所在三角形的三个顶点,并根据它到三个顶点的距离综合确定该点的取值。
这种算法被称为单纯形噪声(Simplex Noise)算法。
坐标变换
由于正三角形中较难计算,需要将其变换到等腰直角三角形,使用如下变换:
(x,y)↦(x+(x+y)F,y+(x+y)F)
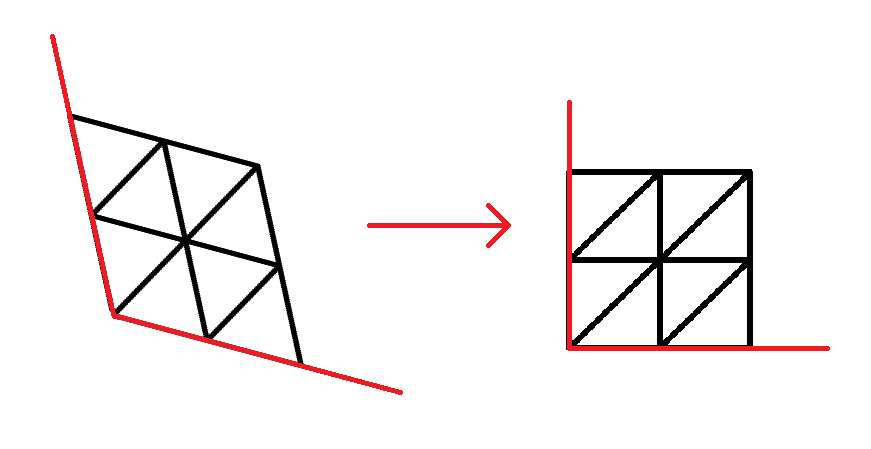
其中 F=23−1。
然后,使用向下取整找到其中一个角
(x′,y′)=(⌊x⌋,⌊y⌋)
然后把这个角变换回去,得到这个角的实际坐标
(x′,y′)↦(x′−(x′+y′)G,y−(x′+y′)G)
其中 G=63−3,通过偏移量即可算出另外两个角。
坐标变换的溢出与末地六边形
大家能够发现,上一节有一些位置标红了。这些位置在源代码中都是整型运算,可能出现溢出现象——这是我们的老朋友了。
若出现了整型溢出,则计算出的三角形会出现极大的偏移。此时,三角形的每一个顶点与插值目标点的距离都会变得极大。
而 MC 用
λi=max{0,0.5−∣PAi∣2}
计算各个顶点的贡献,因此整型溢出之后,由于距离变得极大,三角形每个顶点的贡献都为 0,导致噪声值恒为 0,抑制了地形的生成。
我们可以得到正常区域(大致)的区块坐标方程:
⎩⎨⎧∣x+(x+y)F∣≤231∣y+(x+y)F∣≤231∣x+(x+y)F+y+(x+y)F∣≤231
这是一个六边形区域。
末地晶体结构
众所周知,计算区块的时候是会取整的。而 Mojang 在这个取整上也使用了 32 位整数,于是区块也有了 232 的溢出周期,如下图:
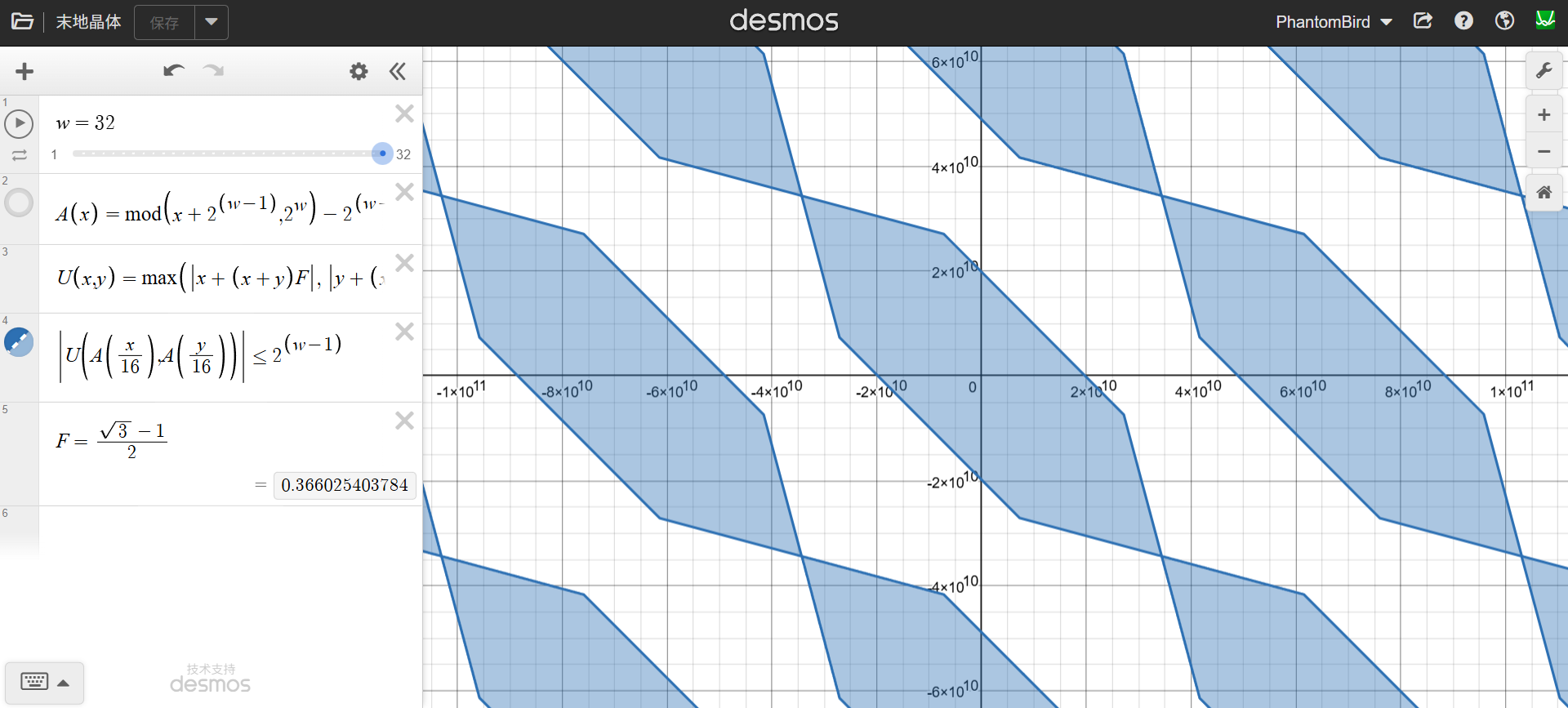
注
由于坐标系不同,在游戏中晶格长边是东北-西南方向的。
最后的问题
截至目前,我仍然无法明晰导致末地晶体结构的函数调用链路。因为确定高度值的函数中,区块坐标是由小块坐标(也是整型)除以 2 得到的。此时坐标的绝对值应当小于等于 230。这就导致晶格形状发生了变化。
然而,UltimateScaler 模组缩放后得到的地形的确表明我们之前的推导无误。因此应该有未知的噪声在起作用。