绝对值的 max 分解是指
∣a∣=max{a,−a}.
相比于将含绝对值的不等式分解为两个不等式,这种分解方法更直接、更紧,且能更好地解决含绝对值的不等式问题。
2024.11.6 提出 max 分解时的例题。
问题
已知 [x2+(m−2)x+∣x2−(m+2)x+2∣]min=0,求 m 的取值范围。
解:
x2+(m−2)x+∣x2−(m+2)x+2∣
=x2+(m−2)x+max{x2−(m+2)x+2,−[x2−(m+2)x+2]}
=max{x2+(m−2)x+[x2−(m+2)x+2],x2+(m−2)x−[x2−(m+2)x+2]}
=max{2(x−1)2,2mx−2}
图象
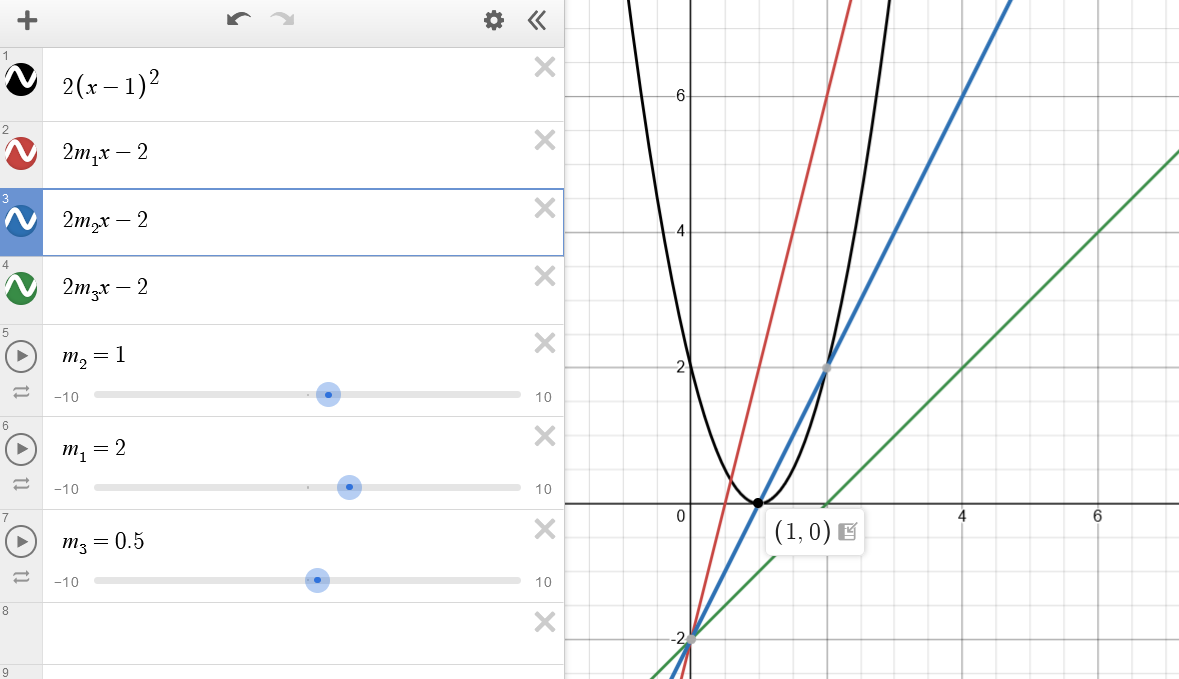
由图象可知 2m×1−2≤0,故 m∈(−∞,1].
问题
若 ∀m>0,m2+∣m−a∣≥49,求 a 的取值范围。
解:∀m>0,
⟺⟺m2+∣m−a∣=m2+max{m−a,a−m}=max{m2+m−a,m2+a−m}≥49,m2+m−a≥49 或 m2+a−m≥49,a≥−m2+m+49 或 a≤m2+m−49.
画出 a-m 图象如下(阴影部分为满足不等式的部分):
图象
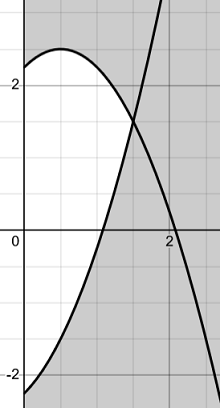
由于任意 m>0 都要满足不等式,即一整条线 a=a0(m>0)都要在区域之内。
于是符合要求的区域如下图红色部分:
图象
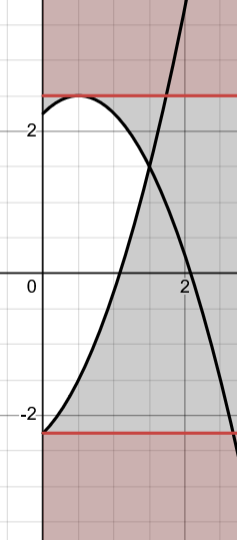
即 a≤−49 或 a≥25.


