为了简化情况，假设琴弦的波为驻波，则有以下方程：

$$y = {\color{red}{A \sin\left( \frac{k \pi x}{L} \right)}} {\color{blue}{\sin (2\pi ft)}}$$

作为近似，我们假设振幅 $A$ 很小。

对某一时刻 $x$ 位置的长度为 $\mathrm{d} x$ 的微元作受力分析，因为振幅很小，所以张力 $T$ 恒定。

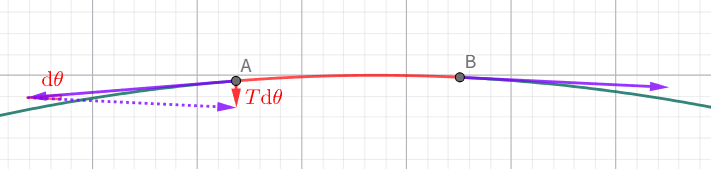
如上图，由几何关系得微元受力为 $T \mathrm{d} \theta \sim T \mathrm{d} \dfrac{\mathrm{d}y}{\mathrm{d}x}$。并且，受力方向垂直于切线，即近似竖直（因为振幅很小）。

由牛顿第二定律，

$$T\mathrm{d} \dfrac{\mathrm{d}y}{\mathrm{d}x} = ma = a \rho S\mathrm{d}x$$

即

$$T \frac{\partial^2 y}{\partial x^2} = \rho S a = \rho S \frac{\partial^2 y}{\partial t^2}$$

于是

$$-T \left(\frac{k \pi}{L}\right)^2 y = -\rho S \left(2\pi f\right)^2 y$$

解得

$$f = \frac{k}{2L} \sqrt{\frac{T}{\rho S}}$$

令上式的 $k$ 为 $1$，即得基频 $\dfrac{1}{2L} \sqrt{\dfrac{T}{\rho S}}$。