外观
FFMP 20240927
约 512 字大约 2 分钟
2024-09-07
有一个网格,一个机器人需要从 (0,0) 出发,每次只能向上或向右走一格,到达终点 (100,100).
(1)若在 (6,6) 处有一个必需物资,机器人必须经过 (6,6),有多少种不同的走法能走到终点?
(2)若 (7,7) 与 (66,10) 两点的网格坏了,不能经过这两点,有多少种不同的走法能走到终点?
由于数字过大,保留答案中的所有组合数。
提示
考虑到排列组合是超纲的,并且这也不是今日FFMP主要考查的内容,因此在此给一些提示。
1.这个问题的简化版:有一个网格,每次只能向上或向右走一格,问有多少种方法,能从 (0,0) 走到 (m,n)?这是一道小学奥数题,答案为 Cm+nm(或等价的Cm+nn)。你可以在你的推导中不加证明地使用这个结论。不用管这个 C 到底是什么符号。
2.乘法原理:如果完成一件事需要分成多个步骤,每个步骤有多种方法,且这些步骤不会相互影响,那么完成这件事的方法数等于各步骤方法数之积。形式化地,若做第 i 步有 mi 种不同的方法(i=1,2,3,…,n),那么完成这件事共有 n=m1m2m2⋯mn 种不同的方法。
答案
(1)
从 (0,0) 走到 (6,6) 共有 C126 种走法;从 (6,6) 走到 (100,100) 相当于从 (0,0) 走到 (94,94),共有 C18894 种走法;
由乘法原理得共有 C126×C18894 种走法
(2)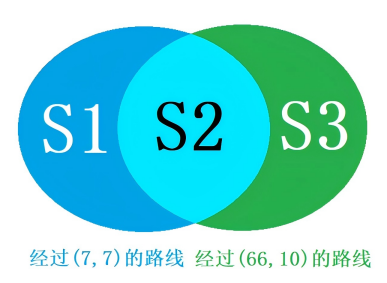
S=C200100
S1+S2=C77×C18693
S2+S3=C7610×C12434
S2=C77×C723×C12434
S−S1−S2−S3=C200100−C77×C18693−C7610×C12434+C77×C723×C12434